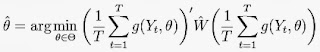GMM and the structural vs. reduced form debate

stolen from Wikipedia

Among this year's economics Nobel laureates is Lars Hansen, who pioneered the generalized method of moments approach for estimating economic models. Tyler Cowen gives a nice summary of Hansen's contributions to economics and finance, and Alex Tabarrok attempts to explain GMM to the layman.

I think that one underappreciated aspect of GMM is that is illustrates how silly the structural vs. reduced form debate is. GMM allows us to estimate equations derived from structural models at low computational cost and with minimal assumptions. We don't have to assume that the entire structural model is "true;" we only have to assume that the functional form of the estimated equation is meaningful relative to the parameters being estimated.

Vocal opponents of structural approaches seem to think that estimating a structural model requires far more heroic assumptions than estimating the typical linear model used in reduced form work. GMM shows that this is not necessarily the case.

Ultimately the difference between reduced form work and a lot of structural estimation work boils down to functional form. Structural approaches choose the functional form of the estimated equation based on a derivation from a structural model. Reduced form approaches choose based on treatment effect concerns, and they typically choose from within the universe of linear or nearly linear functional forms. They both fit the equation to data by minimizing error. I fail to see how one approach is more realistic than the other. It's not immediately obvious that a linear model of anything is a more or less accurate representation of the real world than any other functional form; rather, it likely depends on the research question and the items being measured. It's nice to approach the discipline with a variety of tools so we can find the right tool for each job.